Про
улитку, резинку, и
мысленно - формульное изгаляторство.
Эта
задачка из разряда аналогии апории Зенона про черепаху и Ахиллеса, достаточно
регулярно появляется на многих физических и математических форумах, в массе
блогов. Считается особым шиком доказать во что бы то ни стало, что медленно
ползущую черепаху никогда не догонит быстрее ее передвигающийся человек. С этой
конкретной задачкой про Ахиллеса и черепаху вроде разобрались, опыт опровергает рассуждалки. Но философам от фонаря с
математическим уклонам неймется. В разных вариантах уже с резинкой она все равно возникает
как парадокс, но на деле все равно апория-чушь.
Однажды на уроке информатики в школе, учительница задала нам
следующую задачу:
Улитка начинает свое движение по резинке
длинной 1 метр. Каждый час улитка проползает 1 см, а резинка растягивается на 5
см. Считаем, что длинна улитки не имеет значения. Достигнет ли когда-нибудь
улитка другого конца резинки, и если достигнет, то через сколько часов?
Услышав эту задачу, народ стал выкрикивать готовые решения вроде
«достигнет!», «не достигнет!», а то и «резинка порвёться
раньше» :), на что учительница предложила написать простенькую программу,
которая бы и являлась одновременно решением этой задачи и доказательством его.
То, что растягивание резинки
бесконечно, подразумевается.
Учительница
и программку свою выставила, вот только не пояснила ученикам, что программки не
являются каким бы то ни было доказательством правильности суждений, а тем более с ошибками.
Понятен ли вам парадокс "муравья на резиновом тросе"?
Задает
вопрос один из «продвинутых» блогеров и начинает развивать
тематику абсурдного доказательства.
Как то мы уже с вами обсуждали уже такой парадокс,
который называют либо "Ахиллес и черепаха", либо жучок и резинка, но
прочитав комментарии к тому посту я понял, что мало кто осознал это и вообще
поверил этому.
Товарисчь разницы не понимает, между парадоксом и апорией.
Что у нас по условию?
На старте муравей находится на одном конце резинового жгута. Второй
привязан к автомобилю. И муравей, и автомобиль начинают двигаться одновременно.
Машина едет со скоростью километр в секунду. Муравей ползёт со скоростью один
сантиметр в секунду. Доберётся ли муравей до машины? Это кажется совершенно
невозможным – резина растягивается быстрее, чем движется муравей.
Значит муравей не доберется до машины? Или доберется?
Блогер ![]() biglebowsky напомнил
тогда такую историю.
biglebowsky напомнил
тогда такую историю.
Воспоминания академика Л.Б. Окуня. «Три эпизода», журнал "Природа",
1990, №8, стр.119.
"Великому физику акад. А.Д. Сахарову принадлежит неофициальный рекорд
скорости решения этой задачи.
21 июля 1ь б976 г. Ресторан «Арагви» в Тбилиси, где
происходит торжественный ужин участников международной конференции по физике
высоких энергий (XVIII в серии так называемых Рочестерских
конференций). Много длинных столов. За одним из них я оказался вблизи от Андрея
Дмитриевича. Общий разговор стохастически менял
направление. В какой-то момент заговорили о задачах на сообразительность. И тут
я предложил Андрею Дмитриевичу задачу о жучке на идеальной резине. Суть ее
такова.
Резиновый шнур длиной 1 км одним концом прикреплен к стене, другой у вас в
руке. Жучок начинает ползти по шнуру от стены к вам со скоростью 1 см/сек.
Когда он проползает первый сантиметр, вы удлиняете резину на 1 км, когда он
проползает второй сантиметр, - еще на 1 км, и так каждую секунду. Спрашивается:
доползет ли жучок до вас, и если доползет, то за какое время?
И до, и после этого вечера я давал задачу разным людям. Одним для ее
решения требовалось около часа, другим сутки, третьи оставались твердо
убеждены, что жучок не доползет, а вопрос для времени задается, чтобы навести
на ложный след.
Андрей Дмитриевич переспросил условие задачи и попросил кусочек бумаги. Я дал
ему свой пригласительный билет на банкет, и он тут же без всяких комментариев
написал на обороте решение задачи. На все ушло около минуты."
В статье была фотография того самого пригласительного билета с решением
Сахарова.
пруф
Вообще математически задача достаточно сложная и полное решение ее можно посмотреть
тут или вот тут - Ant on a rubber
rope
Ну, а как бы простыми словами то объяснить?
Да никакими, есть аналогичный опыт с катушкой ниток, которая разматывается,
допустим, на метр, как только
нитку скрутят на такую же катушку с другого конца на пол метра.
Длина свободной нитки между катушками в самом начале один метр.
Смотал полметра, а свободный провис стал
полтора, еще полметра, провис два, еще полметра
провис два с половиной и так далее, наматывать не успеваешь.
Все!!!
Вот что предлагал тогда блогер ![]() mischa_poet:
mischa_poet:
Давайте сначала докажем, что скорость муравья на разных участках ленты
будет разной. Для простоты предположим, что муравей вообще не двигается.
А с какого рожна разная
скорость? Она задана в условиях задачи
Ситуация 1. Муравей сидит на конце ленты, расстояние за ним 0 м,
перед ним 1 метр. Машина проехала 1 метр. Расстояние за муравьем 0 м, перед
муравьем 2 метра. Скорость его ноль
Ситуация 2. Муравей сидит на центре ленты, расстояние за ним 0,5 метра, перед
ним 0,5 метра. Машина проехала 1 метр. Длина ленты стала 2 метра, но центр
остался там же, при этом расстояние за муравьем 1 метр и перед муравьем 1 метр.
Хотя изначально за ним было 0,5 метра. Т.е. за секунду он преодолел 0,5 метра.
И т.д., вы видите, что находясь на разных участках
ленты скорость муравья будет разной, чем ближе к машине, тем выше его скорость.
Давайте облегчим задачу и перенесём центр системы координат на муравья.
Возьмем опять же центр для простоты. Только теперь муравей движется.
0 секунда. Машина относительно муравья будет на расстоянии 50 см
1 секунда. Теперь расстояние будет (50-1)*коэффициент
растяжения. Коэффициент растяжения это цифра которая
показывает во сколько раз увеличивается кусок шнура. Шнур был 1 метр, стал
через секунду 2 метра, соответственно коэффициент растяжения стал равен двум.
Итак расстояние до машины теперь (50-1)*2 или 98
2 секунда. Теперь расстояние будет [(50-1)*2-1]*коэффициент
растяжения. Шнур был 2 метра, стал 3 метра => коэффициент растяжения теперь
будет равен 1,5
Итак расстояние до машины теперь [(50-1)*2-1]*1,5 или
145,5
И вот здесь тот момент который вас смущает, расстояние действительно
увеличивается 50, потом 98, потом 145,5. Но вы не учитываете ускорение это
увеличения, а оно отрицательно. Разница между первым и вторым значением равна
48, тогда как между третьим и вторым она уже 47,5. Дальше будет происходит тоже
самое, прибавка к увеличению расстояния между машиной и муравьем будет
постоянно уменьшатся, пока не станет меньше 1см, в этот момент, расстояние
между машиной и муравьем начнет уменьшаться.
Или вот так еще из примера про Ахиллеса и черепаху:
Пусть она изначально сидит в середине ленты (дадим ей фору) и за каждую секунду
преодолевает ровно половину оставшейся части ленты (все измерения делаются в
долях от длины ленты, которую поэтому можно условно считать равной 1, несмотря
на то, что относительно «неподвижного наблюдателя» лента всё время удлиняется).
Через секунду черепаха будет на отметке 3/4 текущей длины ленты (которая будет
в тот момент равна 11 метрам), еще через секунду — на 7/8, и т. д. Видно, что
черепаха неуклонно приближается к концу ленты.
Ну а теперь итог:

Ну как вам, понятнее стал парадокс или все еще не верится,
что муравей догонит машину?
натуральное жульничество или идиотизм! одно другого стоит.
на растягивающейся непрерывно ленте понятия точки нету, она непрерывно в длину растягивается(точка размазывается), так что пилите гирю с
вашей математикой и волюнтаризмом, потому как и понятие интервала тоже не
определено. Дифференцировать нечего, бескончно
малые не растягиваются. А по сему и
интегрирование невозможно.
И главное!!! Опыты конечно ставить теоретикам в лом. А зря.
Решение находится.
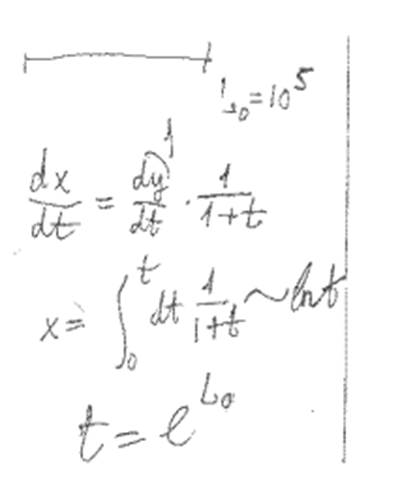
Это отношение скорости удаления Ахиллеса(конец резинки-финиш), к скорости
движения черепахи по растягивающейся ленте, скорости эти постоянны, и не
зависят от пройденных или оставшихся(размазанных) интервалов, заданы в условии
и могут быть измерены без постановки самого опыта.
при равенстве этого отношения единице, скорости равны, а черепаха стоит на
месте относительно Ахиллеса.
Если отношение меньше 1, скорость черепахи больше скорости Ахиллеса и она за
конечное время однозначно достигнет "финиш". Если отношение больше 1, скорость
черепахи меньше скорости Ахиллеса, и достичь "финиша" не получится.
Полная аналогия с отношением скоростей при подъеме или спуске по движущемуся
навстречу эскалатору.
Отношение =1 стоишь на месте, меньше 1 достигаешь верха(низа). больше 1 -
никогда, будет сносить к началу.
А народ типа академика Сахарова, занимающийся такими «экспериментами в
уме», теоретики от фонаря.
Подобная
апория наблюдается и
у господина Эйнштейна----Сам Эйнштейн почти погорел на этой головоломке
https://zen.yandex.ru/media/id/5bffb8bbba3d2500abb6aa17/sam-einshtein-pochti-pogorel-na-etoi-golovolomke-5e07d68bc49f2900ae66577d
Известный психолог Макс Вертгеймер
и не менее известный учёный Альберт Эйнштейн были друзьями. В 1934 году, Вертгеймер отправил Эйнштейну письмо с интересной загадкой.
Автомобилю (речь разумеется идёт о машинах того
времени), нужно сначала ехать в гору, затем спуститься с неё. Расстояние до
вершины горы равно 1 миле. Средняя скорость этой машины, при подъёме в гору
равна 15 миль в час. Расстояние спуска с горы так же равно 1 миле. Скорость,
которую способна развить машина, двигаясь вниз, вероятно может превысить 15
миль в час.
Вопрос: с
какой скоростью должен двигаться автомобиль с горы, чтобы средняя скорость
всего пути (2 мили), составила 30 миль в час?
Прежде, чем я расскажу решение этой
головоломки, немного предыстории.
Как я уже упомянул выше, загадка была
отправлена письмом, в 1934 году. Альберт Эйнштейн стал лауреатом Нобелевской
премии по физике в 1921 году. Ещё в 1905 году, этот выдающийся учёный сделал
несколько открытий подряд, среди которых:
·
объяснение фотоэлектрического эффекта
·
Броуновское движение
·
Специальная теория относительности
·
Эквивалентность массы и энергии E=mc2
Каждое из этих открытий в отдельности, могло бы
стать работой всей жизни, но он создал все четыре, всего за один год. Вы можете
подумать, что если и был человек, способный решить любую головоломку в уме, то
это Альберт Энштейн. Но, как оказалось, даже у него
возникли проблемы с этой задачкой. Как писал учёный, он не увидел подвоха, пока
не вычислил ответ.
Решение
задачи:
Вначале, давайте найдём время, требуемое для
преодоления пути в 2 мили, со средней скоростью 30 миль в час. Для этого
составим уравнение:
30 миль в час=2 мили/t (общее) в чем прикол? А это время равномерного движения на обоих
участках с одной и той же скоростью! Автор сразу накосячил,
волюнтаристски умыкнул скорость первого участка в условии задачи.
Найдём время. Сначала получаем 1/15 часа и так
как в часе 60 минут, то находим общее время:
Вот у него и появилось общее
время=4 мин.
Теперь, давайте найдём время, которое требуется
машине, чтобы заехать на гору. Машина преодолевает 1 милю, со средней скоростью
15 миль в час.
Время в гору=4 мин но не при
скорости 30, а скорости 15….на двух участках движение
не равномерное!
В итоге, мы нашли, что время для подъёма в гору
равно 4 минутам, так же как и общее время пути
составило 4 минуты. То есть времени на спуск с горы остаётся ровно 0
минут.
Поразительный результат, не правда ли?
Получается, что машине невозможно преодолеть расстояние в 2
мили, чтобы машина ехала в среднем 30 миль в час, покуда на спуск с горы
остаётся 0 минут. Это было бы возможно только в одном случае, если бы машина
ехала со сверхсветовой скоростью.
Восхитительная маленькая головоломка, которая
понравилась даже Энштейну!
тупизна очевидная, вы на опыте можете проверитЬ! ваша(эйн цвай драй штайн)
хрень и
манипулирование понятием среднего, запудривание мозгов нереальными 2 мили делить на 30
не делятся, апория типа Зенона, порете тут в массе
своей физ мат(нецензура) чепуху.
Движение неравномерное на двух
участках, а вот такая хрень превращает его в движение равномерное-с одинаковой
скоростью, что убивает условие задачи.
И все потому, что первый участок проходится
за большее время, чем второй! средняя скорость вычисляется исходя из двух
скоростей! а не назначается !И при ее задании вычисляется скорость на втором
участке!
(45+15)/2=30
х=2*30-15 , где двоечка 2 мили или два участка,
причем любых. Все решается чисто уравнением со скоростями! Без времен, которые
определяются из скоростей отдельно.
время подъема=4 мин
время спуска=1.33 минуты. общее время
4+1.33=5.33 мин.
много простачков желаете облапошитЬ! опыт в лом ставить.
Вот еще одна апория от физмата
http://fatyf.aiq.ru/velocty.htm про мразматику от
физмата.
Фатьянов А.В. Спб. 17.12.2019