Ньютоновская
сфера и невесомость тел внутри нее.
Отдел XII
О притягательных силах сферических тел
Предложение LXX
теоремa XXX « Математические начала натуральной
философии» стр.244 http://fatyf.aiq.ru/newton.djvu
Утверждение Ньютона о невесомости внутри полой
сферы с представленным
геометрическим доказательством не является верным!
Развернутое доказательство см.
https://elementy.ru/posters/gravity/6
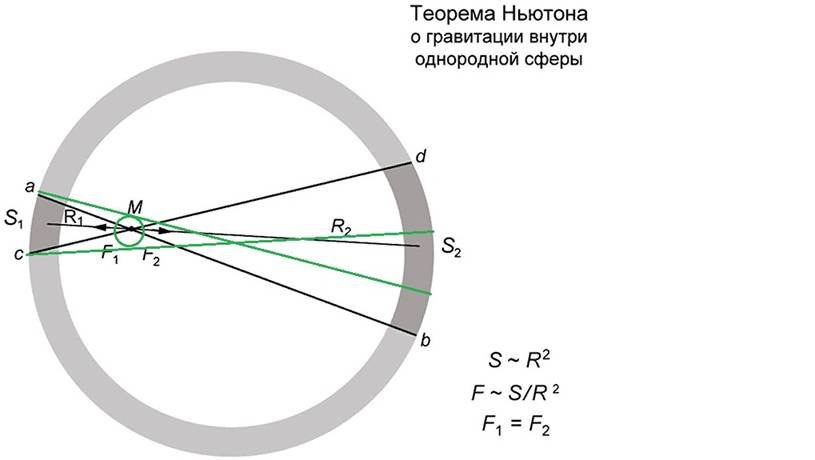
Некоторые называют это парадоксом, дескать: «теорема доказана для произвольной точки, а это значит, что любая точка тела любой конфигурации будет невесома внутри сферы. это не сразу укладывается в голове, но мы и говорим о таких вещах, которые не сразу укладываются в рамки здравого смысла.»
Интуитивно чувствуется подвох, а что тут не так, раз не укладывается здравым смыслом
в голове!
Это не парадокс, это ошибка!
Тут Ньютон стал заложником своего точечного представления массы. Им введено
упрощение, допускающее сведение массы тела в точку, когда размеры тел на
порядки меньше расстояния между ними.
Это начальное условие нее оговорено при доказательстве!
Чем хорош Ньютон, он не стал рисовать сферы с размерами(толщина никакая и масса в точках на поверхности), а нарисовал ее сечение в плоскости. А тем самым ушел от объемов и площадей поверхности. Тело внутри сферической поверхности тоже точка, получается, что можно расположив тело с массой в виде точки в плоскости сечения перейти к чисто геометрической(планиметрия!) задачке. Масса тел из доказательства пропала! Это и есть пренебрежение физикой.
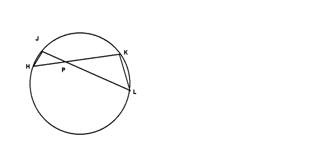
После сказочного исчезновения массы, легко с помощью подобных треугольников получаются пропорции. Но, Ньютон скачкообразно возвращается от планиметрии к стереометрии и утверждает что «весьма малые части поверхности сферы», а не дуги окружности, «прилегающие» к хордам HJ KL? и «ограниченные прямыми HK JL, проходящими через» точечное тело P будут находиться в отношении квадратов длин PH PK. ( Откуда квадраты длин взялись? это погон под площадь или закон обратных квадратов?) Следовательно силы притяжения этих малых частей дуг(поверхностей у Ньютона) на точку Р между собою равны(часть поверхности это площадь! Она имеет размерность м2, такую же как в отношении и сокращается!), ибо эти силы прямо пропорциональны этим поверхностям и обратно пропорциональны квадратам расстояний.???
В чем беда? На дугах находится не одна точка, и не одна точечная масса, в случае «весьма малых» дуга превращается в точку и вся геометрия насмарку - в тех же пропорциях «весьма малых» треугольники с пропорциональностями становятся прямой, проведенной через две точечные массы к одной точечной массе!
У Ньютона получается несоответствие отношения множества к одному! Или отношение «весьма малой» длины дуги(площади поверхности) к точке, у которой нет измерения.
Вот тут и появляется здравый смысл! На какой половине окружности массы больше? И чье суммарное действие сильнее. В предельном случае масса внутри касается поверхности(окружности по чертежу) и две точечные массы сливаются в одну,
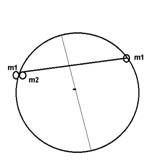
спрашивается, сумма двух масс m1+m2 будет равна точечной массе m1 на противоположной стороне? Однозначно нет. Как не проводи прямые в любом направлении неравенство соблюдается. Следовательно и сила притяжения суммы масс больше, а это означает, что при любом смещении точечной массы равновесия относительно центра не будет и относительно линии деления окружности пополам, а будет дисбаланс сил и отсутствие невесомости везде, кроме центра.
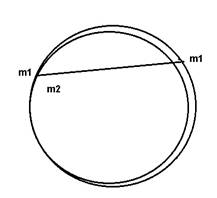
Еще один предельный случай, дисбаланс налицо!
чем масса и размер внутреннего тела больше, и чем меньше расстояние до внутренней поверхности тем больше суммарное действие одной половины сферы на другую! Простыми словами без математики и стереометрии с интегралами. дисбаланс масс в любом теле приводит к дисбалансу всей системы. соответственно и к дисбалансу сил. Сумма элементарных масс всегда больше ее части, а это означает, что по любой прямой проходящей через массу не по центру сумма масс всегда больше массы на противоположном конце.
В приведенном выше в качестве ссылки «доказательстве»
моментально ошибку нашел! масса на сфере не точечная, а
масса внутри точечная! и не действует то же самое соотношение: m1 = k2·m2 стоит
придать размер(шар) точке и вся геометрия
разваливается!
для двух масс неравнозначные начальные условия!
возникают в результате геометрического построения от точки к массе точек
воображаемых упрощений!
извольте господа работать с точечными массами или реально указывать размер тел
и длины!
не будет невесомости при сложении точечных масс, одна из которых смещена(в пределе касается внутренней поверхности) относительно
центра сферы по линии действия с учетом закона обратных квадратов. по- любому
дисбаланс сил, если масса не в центре
количество массы с одной стороны всегда больше массы с противоположной. можно
размазать объемную массу по одной половине сферы для пущего эффекта, никто не
запрещает пока... орудовать формой и местом..

Далее следует еще одна теорема.
Предложение LXXI. Теорема XXXI , стр. 245.
«При тех же предположениях утверждаю, что частица, находящаяся
вне сферической поверхности, притягивается к центру сферы с силою,
обратно пропорциональною квадрату ее расстояния до центра сферы.»
С таким же игнорированием начального условия больших расстояний и малых размеров тел. Игнорируется и масса чисто геометрически! Игнорируются размеры.
Но в процессе доказательства во всю используется понятие бесконечно малых, применяемого как попало, к углам и перпендикулярам и не соблюдении пропорциональных изменений других элементов геометрического построения!
Если вперемежку использовать такие приемы, что недопустимо, заранее закладывая невероятные допущения, математика такая приводит к неправильным выводам.
Вся масса шара сводится в невероятную точку при полном игнорировании его размеров и взаимодействия элементарных (весьма малых) масс друг с другом и телом вне шара,
как точечного или как имеющего размер.
Продолжение следует.
Фатьянов А.В. Спб-Воронеж 3.11.2019