При обсуждениях мне пришлось столкнуть вот с таким. Оппонент решил ткнуть носом и обосновать период по другой методике, нежеле той, которая имелась у Гюйгенса.
Конечно, спорить с каждым случаем достаточно сложное занятие чисто по временным затратам. Если еще и торопишься, то неизбежны ошибки, я их не боюсь и готов признать, если таковые найдутся.
Приходится иногда напоминать, что я рассматриваю только первоначальные доказательства, а не вторичные, хоть даже и через двести, триста лет. В принципе Достаточно одной зацепки, чтоб найти слабое место и развалить все здание на корню, поскольку это фундамент всего остального, позднейших наслоений, при помощи чего пытаются обосновать справедливость самого основного, и явно ошибочного,
Что и сделано в данной статье.
Однако умельцы от академической физ—мат-тех направленности, подсовывают иногда интересный материал, который никак пропустить невозможно.
В пылу обсуждения мне заявили, что период колебаний тот же самый (с 2пи) у пружинного маятника, и у колебательного контура.
Функция
f(t) является периодической
с периодом Т,
если при всех значениях её аргумента t
выполняется соотношение
f(t+T)=f(t)
В частности, функция f(t)=sin(pt )
будет периодической с периодом T=2Пи / p
Проводим проверку периодичности, т.е. проверку выполнения условия sin (pt)= sin(
p*(t+T) )
sin (pt)= sin(p* (t+T)
)=sin (pt+pT) =sin(pt + 2Пи p/p ) = sin
(pt+ 2Пи) что и тр-сь
доказать
Таким образом, синусоида будет возвращаться к своему состоянию (совершать
полное колебание) через время
T= 2Пи / p
Движение описывается одним и тем же уравнением
для угла отклонения Fi математического маятника
d2Fi / dt2= - l/g Fi
или
для смещения X груза пружинного маятника
d2X / dt2 = - k/m X
или для напряжения U на конденсаторе C колебательного контура LC
d2U/dt2 = - (1/LC) U
Потому решение всех трех задач о колебаниях будет подобным
Fi, X, U = sin (pt)
где
p= sqrt (
g/l ) для
математического
p=sqrt ( k/m ) для пружинного
p=sqrt ( 1/LC ) для колебательного контура
Соответственно периодом будет
для математического 2Пи *sqrt ( l/g )
для пружинного 2Пи *sqrt ( m/k )
для колебательного контура 2Пи *sqrt (LC )
возражения не принимаются.
Только один вопрос, а с чего вы взяли, что колебание маятника синусоида? Никогда!!!!!!
Замечательно математики обходятся без физики. У них движение по окружности ничем не отличается от колебания, Они даже саму статью прочесть не в состоянии, где про это принципиальное различие и говориться в самом начале.
Повторимся.
Движение по окружности равномерное и якобы движение по синусоиде не являются возвратно-поступательными. Там нет торможений с остановками, нет угловых ускорений изменяющих свое направление.
И подкладывание движущегося равномерно листка бумаги под кончик маятника, рисующего якобы синусоиду, является уже совместным движением двух тел, это, во-первых. И, во-вторых, маятник собственно не движется по кривой, он просто рисует, эта линия ---художественное произведение при помощи маятника с использованием приспособления, а не он ее творение.
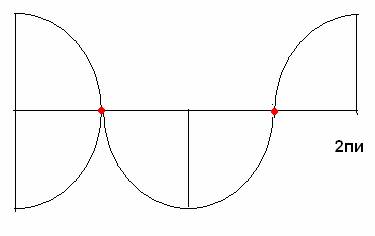
А вот давайте и разберем, что может изображать эта кривая для начала.
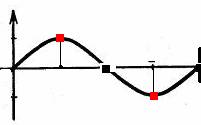
Красным обозначена точка равновесия, которую маятник проходит дважды.
Сам угол отклонения может быть любым, и путь, который маятник проходит по дуге окружности, заданной этим углом, тоже может быть любым. И именно аналог этого полного пути рисует маятник и никакого другого, это часть окружности в ту и другую сторону. И они, половики, естественно равны. Но Никаких тут периодов 2пи от синуса не наблюдается, нет туда обратно 360 градусов, кроме одного единственного случая приведенного в статье.
То есть с полным правом можем дать такое пояснение:
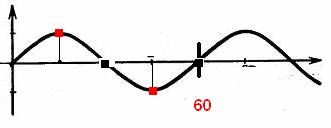
30 градусов туда сюда, и забыть про 2пи, поскольку маятник никто из этого положения не отпускает. Это уже не движение по кругу. Это уже не функция синус в привычном нам изложении. Это 1/6 или 1 какая угодно часть окружности. Это более общий случай. Можно в качестве аргумента использовать и угол, как отношение длины дуги к радиусу. L=R j , но не наглядно.
А что такое синус, это отношение сторон треугольника.
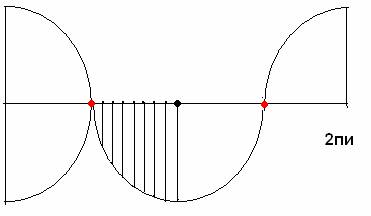
Я лично тут треугольников пока не наблюдаю, аппроксимировать прямыми отрезками ничего не собираюсь. Я наблюдаю кусок окружности либо растянутой, либо стянутой в той или иной степени, из-за разной скорости движения ленты. Если синхронизировать общую скорость движения ленты с общей скоростью качания маятника в пределах данного угла, пускай постоянного, то есть протягивать ленту на расстояние одинаковое с пройденным расстоянием по хорде, то мы опытным путем получим реальную картинку характера изменения пути или углового смещения. Пока только картинку.
Вот и покажем это наглядно.
Для случая половины окружности.
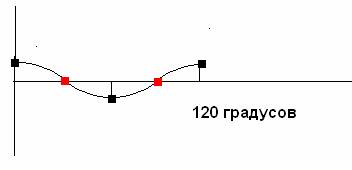
Синусоиду это мало напоминает, согласитесь…только общими очертаниями, поскольку это куски дуги окружности. Чуть получше это будет ее напоминать, если выбрать угол, к примеру, 30 градусов. Диаметр окружности тот же самый.
Не похоже, зато точно. Путь другой. Красным показано положение равновесия, черным крайнее положение при отклонении. Именно по такой кривой движется маятник и нет смысла ее аппроксимировать, если известен угол и радиус, или угол и длина дуги.
Период этого движения равен 120 градусам.
На основную часть вопроса мы уже ответили. Периодичность не характеризуется числом 2пи. Периодичность характеризуется самим видом протекания процесса и повторяемостью циклов, а в качестве параметров выступают скорость и ускорение. Время и путь.
Поэтому все, что касается колебательных процессов, цельнотянуто из кинематики Гюйгенса, а она порочна в принципе.
Пружинный маятник совершает возвратно-поступательное движение и тригонометрией тут вообще не пахнет, поэтому период его аналогичен простому маятнику, T=t/n
В колебательном контуре, ток движется так же возвратно поступательно, и определение периода вполне может быть осуществлено при помощи секундомера и амперметра, по максимальному отклонению стрелки. Тут тоже не наблюдается никакой тригонометрии, а зависит от времени прохождения тока по цепи.
И тупо все сводить к одному движению по кругу, себе дороже.
Стандартная синусоида лишь частный случай при движении по кругу и является приближением, а нам все-таки хочется точно. А дальше уже дело техники, как вывести аналитику ускорения по дуге окружности. По аналогии http://fatyf.0fees.us/cinema.htm Продолжение следует. Кто не успел, я не виноват. А предложения были.
Продолжение.
Оно видно, что перемещение точки по линии между двумя крайними положениями маятника (хорде окружности), является равномерным, а движение по дуге ускоренным. Пути разные за одни интервалы времени. Поэтому на ленте можно заранее расставить метки.
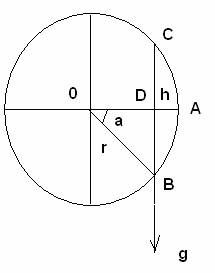
А раз эти метки находятся на одинаковом временном интервале, а перемещение равномерное, то задача решается простым геометрическим способом. Нам надо просто вычислить половину длины дуги отсекаемой хордой в точке приложения ускорения(силы), которое при отпускании маятника уменьшается с набором угловой(либо окружной) скорости по этой дуге. Рассмотрим отклонения маятника в 90 градусов, как предельный.
Длина половины хорды СВ = 2*r* sin(а) = 2*(2*r*h-h2 )1/2
длина дуги AB = π*r*(α/180o)/2 = 0,017453*r*a/2 ≈ (c2+(16/3)*h2)1/2
http://www.dpva.info/Guide/GuideMathematics/GuideMathematicsFiguresTables/ArcLenghtNeedle/
h –это расстояние между метками. Они равны, так как перемещение без ускорений за равные интервалы времени.
Дуга АВ—путь, который проходит маятник за указанный промежуток времени. Обозначим как s.
Движение равноускоренное(равнозамедленное после прохождения точки равновесия), так как подвес нерастяжимый и другие сторонние ускорения не рассматриваются.
Потому ускорение свободного падения уменьшается плоть до нуля в точке равновесия и возрастает до нормального значения в верхней точке подъема.
Компенсация этого ускорения и есть искомое угловое ускорение.
Расчет ведется в соответствии с теорией изложенной в http://fatyf.0fees.us/cinema.htm О равноускоренном движении.